功能
- 功能简介
- 更多系统
400-118-8335
目前已有研究表明,一些单纯建立在混沌系统上的置乱方法已有了破解方法,因而必须结合其他置乱方法来提高混沌动力系统的图像置乱性能。鉴于此,我们提出了一种基于混沌二值密钥的、依据格雷码表分块置乱的数字图像加密算法。该方法首先将图像分成几幅子图相互均匀散布(称为“洗牌”),然后再将各子图按照格雷码表顺序进行分段置乱,置乱次数由参数设置。
一、混沌系统
目前,绝大多数文献中使用的混沌动力系统是一维离散时间非线性动力系统Lohistic映射和k阶Chebyshev映射。
(1)Lohistic映射
Lohistic动力系统可谓目前最简单、最被广泛研究和应用的混沌动力系统,其方程定义如下:
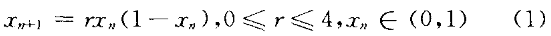
其中,r为分支参数,当O≤r≤3. 569 945 972...时,该动力系统因从稳定状态到分叉而产生倍周期;当3. 569 945 972...<r≤4时,该动力系统进入混沌状态。
通过简单变量替换,式(1)可以定义到(-1,1)区间:
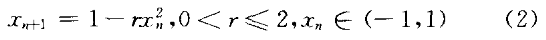
(2)k阶Chebyshev映射
k阶Chebyshev映射是另一类简单的以阶数为参数的映射,其定义如下:
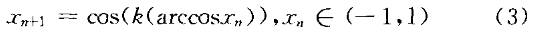
在r=2的满射条件下,式(1)和式(4)是拓扑共轭的,即它们不仅可以被视为动力状态相同的系统,而且其生成序列的概率密度也相同,即:
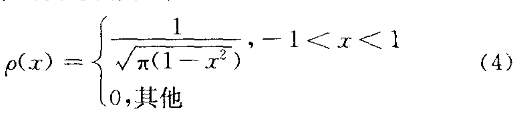
从式(4)可以看出,由于Logistic和Chebyshev映射生成的混沌序列具有遍历性,同时它们还具有δ—like型自相关函数和零的互相关函数,并且具有初值敏感性,因而可以提供数量众多、非相关、类随机而又可确定、可再生的混沌序列。其非常大的周期性和优良的随机性,不仅非常适合产生符合安全要求的序列密码,而且可以提供数量众多的密钥,因而可以很好地被应用于各种混沌保密通信系统中。
本文在具体生成混沌二值密钥时采用共用初始密钥,由Logistic和Chebyshev映射交替或迭代生成二进制密钥流的方法。由于Logistic映射和hebyshev映射在表达式结构上相异程度很大,所以其动力特征退化或平凡密钥具有相似性的概率极小,因而可产生质量较高的混沌二值密钥流。
二、数字图像加密算法
1、 格雷码表设计
格雷码与普通二进制代码相比的最大特点是其相邻两个代码之间只有一位数据发生变化,即只有一位码元不同(此特点通常称作“逻辑相邻性”)。有资料曾提出了利用FASS曲线和Hilbert曲线遍历图像中的所有点以生成一幅新的“杂乱’’图像的图像置乱加密思想。该加密算法利用了这些曲线的充满空间( Space- Fill-ing)、非自交(Sclf-Aroiding)、自相似(Sclf-Sirnilar)等特性,多次置乱的加密效果良好,但要求设计人员有坚实的数学功底,计算复杂度也相对较高。而依靠数字逻辑的基本工具——卡诺图(Karnaugh Map)的帮助,设计3位、4位及多位格雷码表无论对设计人员还是计算机软硬件实现都是非常容易的。
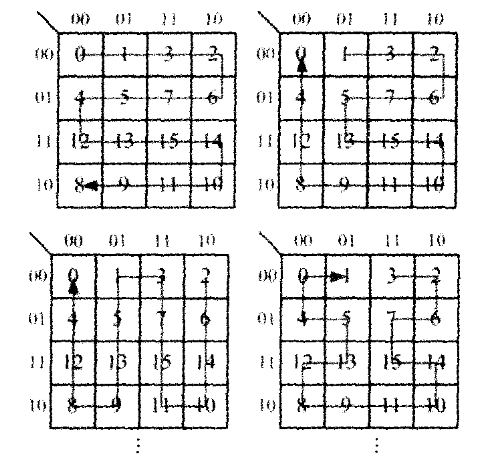
上图所示即为依据4位卡诺图,从不同点(即算法中的‘种子’)切人生成一张格雷码表(表1)的实例。
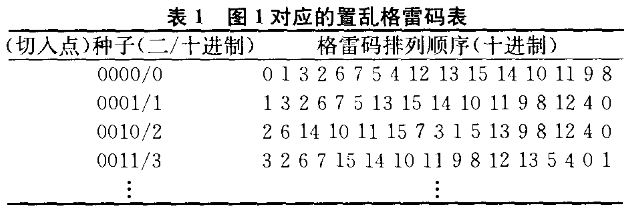 实际上,依据卡诺图的性质,4位卡诺图中任一点(即‘种子’)有四个相邻码,因而可有四种格雷码排列顺序;5位卡诺图中任一点(即‘种子’)有五个相邻码,因而可有五种格雷码排列顺序。依此类推可知:
实际上,依据卡诺图的性质,4位卡诺图中任一点(即‘种子’)有四个相邻码,因而可有四种格雷码排列顺序;5位卡诺图中任一点(即‘种子’)有五个相邻码,因而可有五种格雷码排列顺序。依此类推可知:
n位二进制数的格雷码排列方式共有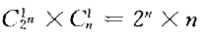 种,每一种对应一张格雷码置乱码表;而且,随着n的增加,数据流分段划分越小,置乱码表越复杂,加密效果越好,安全性越高。由于本加密算法是对称加密算法,双方只要约定了相同的码表即可进行正确的加解密信息传输。该码表亦可依据密钥随机生成和定期更换,以更好地提高安全性。
种,每一种对应一张格雷码置乱码表;而且,随着n的增加,数据流分段划分越小,置乱码表越复杂,加密效果越好,安全性越高。由于本加密算法是对称加密算法,双方只要约定了相同的码表即可进行正确的加解密信息传输。该码表亦可依据密钥随机生成和定期更换,以更好地提高安全性。
2、总体算法描述
如前所述,数字图像的置乱一般可以在其位置空间、色彩空间或频率空间上进行,置乱的目的是将图像像素的位置或像素的颜色“打乱”,将原始图像变换成一个杂乱无章的新图像。
本算法是在图像空间位置上进行的完全加密算法,适用于各种索引图像、灰度图像和真彩图像文件加密。若考虑将图像数据矩阵先与混沌二值密钥进行按位异或加密,则可更好地提高抵抗已知明文攻击的能力。
(1)加密算法实现
设被置乱图像大小为2m X 2n,m、z∈N。
Step l输入参数:输入原始待加密图像文件名)inFileName)、加密后图像文件输出名) outFileName)、Logistic混沌映射分支参数)r)、Chebyshev混沌映射阶数(k)、加密密钥) x0)、图像分块数(k),加密轮数(mc)和所取格雷码位数(nc)。
Step 2生成长度为N的混沌二值密钥序列L:根据输入参数,由Logistic映射和Chebyshev映射相互迭代生成混沌实值序列{lk,k=1,2,3,…,N},生成过程中Chebyshev映射的输出取绝对值,根据阈值法(如设r=0.5,若lk≥0.5,lk=1,否则lk=0)将实值序列转换成二值密钥序列{lk,k=1,2,3,…,N}。若图像分块数、加密轮数和格雷码位数较小,序列长度N=)4+kc×nc),每轮密钥长度mcLen=4+kc×nc,如当kc=4,nc=4,mc=10时,混沌二值密钥序列长度N=)4+4×4)× 10=200,每轮密钥长度mclen=20,当这些参数数值较大时,如加密轮数mc= 30,此时可取固定长度N为128、256或512等等。
Step 3将原图像分块进行均匀散布(即“洗牌”):
a、首先得到文件名为inFileName的图像的句柄(h)(CData图像数据矩阵y)。
b、下面以k=4为例讲述图像分块散布过程:
①将y等分为四幅子冈,将这些子图按左上,左下、右上、右下四个方向分别标记为Pl、P2、P3、P4。
②从本轮密钥的前四位提取出散布种子zi,如zi='0101'等。
③从P1、P2、P3、P4中两两选取子图相互进行均匀散布,则共有P4= 24种,从中约定16种方式;如=‘0000’,P1散布到P2中,P3散布到P4中;i=‘oooi’,P1散布到P2中,P4散布到P3
中,等等。“散布”操作可用下式描述:将一个子图P=(plk)m×n均匀散布到另一个子图像Q=(plk)m×n中去,即Fi,j= ,F=(f,ij)m×2n为置乱后图像,kc>4的散布过程可参照kc=4的过程,唯一的区别是约定从砖:p=(kc)!中选取16种散布方式。
,F=(f,ij)m×2n为置乱后图像,kc>4的散布过程可参照kc=4的过程,唯一的区别是约定从砖:p=(kc)!中选取16种散布方式。
Step 4对均匀散布后的各子图进行格雷码表分段置乱:
a、将均匀散布后的图像再分成kc一幅子图。
b、将每幅子图分成2w段,按照上节中所述nc位格雷码表进行分段置乱(为不占用计算机内存空间,nc位格雷码表依据约定参数随机生成)。每帽子图的置乱切人点(即“种子”)从本轮密钥的第5~kc ×nc位每nc位依次选取。
Step5重复Step3和Step4,直至完成mc轮加密过程。
Step6显示加密后图像,将加密图像保存为文件,加密过程结束。
(2)解密算法实现
由于是对称算法,用户输入正确的解密密钥)jx0)后,将加密算法逆向运算,即可获得解密图像。加解密流程如图所示。
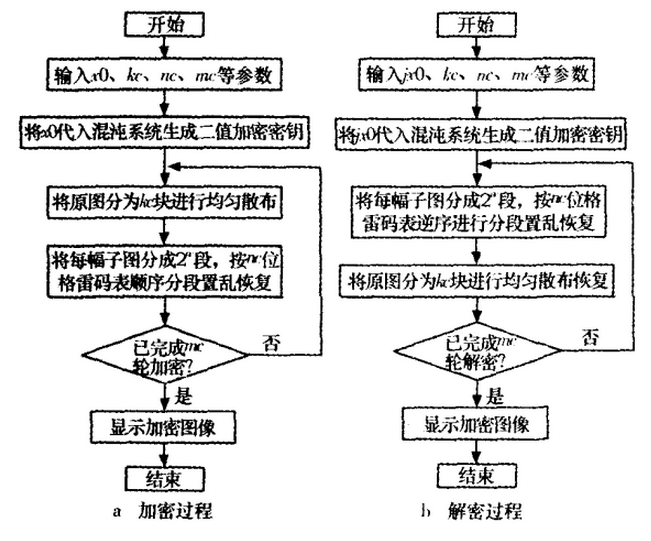
小知识之格雷码
格雷码是一种绝对编码方式,典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,虽然自然二进制码可以直接由数/模转换器转换成模拟信号,但在某些情况,例如从十进制的3转换为4时二进制码的每一位都要变,能使数字电路产生很大的尖峰电流脉冲。

全球著名减震器制造商——天纳克携手安企神共筑安全制造新防线
天纳克(北京)汽车减振器有限公司天纳克(北京)汽车减振器有限公司成立于1995年,是天纳克在中国最早投资的合资企业。公司集设计、开发、生产及销售汽车减振器于一身。作为天纳克全球网络的一部分,能充分享受天纳克全球的技术积累经验和国际领先的设计理念,加之先进的生产设备和工艺技术。天纳克(北京)汽车减振器有限公司完全能保证为...

筑牢安全防线:安企神企业助力特种设备机械企业数据防泄密解决方案
西安苛菲特机械设备有限公司 西安苛菲特机械设备有限公司致力于特种设备的发展,专业从事特种设备的研发、制造和销售。目前已成为有色冶金特种设备、大型船舶特种设备、煤化工特种设备的领军品牌,并在业内得到了“ 特种设备专家”的称号。公司以打造国内一流特种设备为使命,主要产品定型为高品质特种(高温、高压、高合金)流量控...

安企神软件:三峡大学数据安全的坚实后盾与合作伙伴
学校介绍三峡大学是经国家教育部批准,由原武汉水利电力大学(宜昌)和原湖北三峡学院于2000年5月25日合并组建。2018年,学校被省人民政府列为“国内一流大学建设高校”,水利工程、土木工程、电气工程等3个学科被列为“国内一流学科建设学科”;目前,三峡大学已发展成为水利电力特色与优势比较明显、综合办学实力较强、享有较高社...

零部件企业数据保卫战:安企神软件如何筑起防泄密铜墙铁壁
瑞安市特迩翡汽车配件有限公司企业背景瑞安市戴尔菲汽车零部件有限公司一直致力于高共轨电喷(EFI)发动机和SCR排气系统的研发。通过了16949质量管理体系和CE认证,公司具备自主开发汽车电子系统和核心软件的技术能力。公司力争成为以市场为导向、以技术为支撑、以质量为先、以人才为本的知名创新型企业。产品包括:氮氧化物传感器...

强强联合!安企神软件携手瀚颐共筑汽车行业终端安全防线
瀚颐上海汽车电子科技有限公司EAST瀚颐中国团队成立于2015年。是国际AUTOSAR软件联盟的研发伙伴单位。具备汽车电子硬件设计、软件开发、CAN网络集成、系统集成测试以及项目管理的全面研发能力。专注于汽车电子以及相关产业并拥有25年以上的专业经验,拥有来自于德国和中国业内专家和高管组成的顾问团队,并向全球汽车行业客...