本文简介：针对无线宽带系统面临的窃听问题，提出一种基于信道时域弱特征随机加扰的物理层加密算法。一、无线宽带系统加密模型无线宽带系统加密模型主要包括Alice、Bob和Eve三方面，如图l所示。其中，Alice是发送用户，Bob是授权接收用户，Eve作为窃听用户只接收信息，不发送任何信息。在实际通信中，Bob首先向Alice发送未加密的请求信息，该请求信息同时包含用于信道估计的训练序列：Alice接受请求，并
针对无线宽带系统面临的窃听问题，提出一种基于信道时域弱特征随机加扰的物理层加密算法。
一、无线宽带系统加密模型
无线宽带系统加密模型主要包括Alice、Bob和Eve三方面，如图l所示。其中，Alice是发送用户，Bob是授权接收用户，Eve作为窃听用户只接收信息，不发送任何信息。
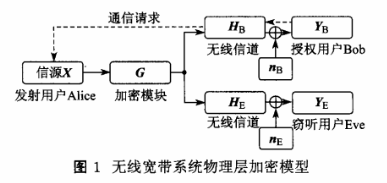
在实际通信中，Bob首先向Alice发送未加密的请求信息，该请求信息同时包含用于信道估计的训练序列：Alice接受请求，并根据接收到的训练序列估计它们之间的信道时域特征。根据互易定理，在信道慢变的情况下，可以认为Alice和Bob之间的收发信道相同．因此，Alice可以根据估计到的信道时域特征对即将发送给Bob的信息进行加密，加密模块是根据Alice和Bob之间的信道特征设计的，加密后的信息经过Alice和Bob之间的信道后趋于稳定，因此Bob无需知道Alice是如何加密的即可直接完成正常解密，获得通信内容，而Eve与Bob的信道特征不同，接收到的是一个随机变化的加密信号，无法正确解出Alice发送的信息，在图1所示加密系统模型中，经过编码之后Alice的发送信号为X=[XI,x2…xM]T，元素观是独立同分布的，在没有信道噪声的情况下，Bob接收信号YB=[Y1y2…ybM]T可以表示为：
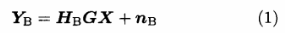
同样，Eve接收信号YE - [YelYe2 …yeM]T可以表示为：
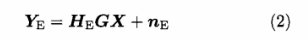
式中，HB和HE分别为Bob和Eve的信道时域特征矩阵，为非奇异的Toeplitz矩阵，nB和Eve为信道高斯白噪声。
G为加密模块的矩阵表示，主要用于和HB共同形成稳定的信道HBG;而与HE共同形成随机快变的信道Hb。从而Bob接收到的有用信息量大于Eve，系统保密容量大于0，但因为HB和HE均为非奇异矩阵，HBG恒定与HEG随机变化不可能同时成立，所以如何设计算法，为G构造可行的冗余空间是需要完成的工作。
二、基于弱特征随机加扰的加密算法
本文算法通过对信道矩阵HB进行特征值分解，得到多个并行的子信道，选择其中具有强特征的子信道发送有用信息，将最弱特征的子信道构成快速时变随机信道，从而得到加密矩阵G可行的冗余空间。
1、信道时域弱特征提取
对HB做特征值分解，则有：
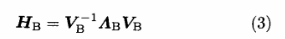
式中，AB为对角阵，且主对角线上的元素按照特征强弱（特征值模值大小）进行排列，VB为可逆矩阵，如下所示：
且有VB-I VB=E，其中E为单位矩阵。
于是Bob的接收信号可以表示为：
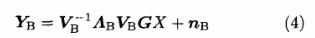
为了保证加密效果的同时尽可能地使系统保持较高的传输速率，选取具有强特征AB，=diag(A61，沁2，…，沁M_i，O)的前M-1个子信道传递有用信息，而选取具有最弱特征以g=diag(0，0，…，O，入bM)的子信道构成随机快变信道，令AB=AB，+Ae，则Bob端接收信号可以分解为：
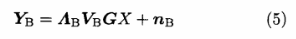
式中，AB，VBGX是由强特征构成的稳定信道，用来传送有用信息．令AB，'VBG为常数矩阵C:第2项AeVBG是由弱特征构成的部分，形成随机信道，造成对Eve的随机干扰。
对Eve的信道矩阵同样进行特征值分解HE=VE-1AEVE，接收时也与Bob作相同处理，则Eve的接收信号可以表示为：
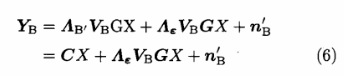
式中，Eve接收信号的系数矩阵AEVEG是随机变化的，用R表示．n乞为V乘以nE之后的结果，n乞～N(O，UE21)。
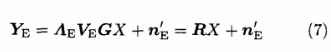
2、加密矩阵设计
简单起见，选取常数矩阵C为对角矩阵，表示为C= diag(cl1,C22，…，CM-lM-I,0)。
为了不失一般性，以M=3为例作进一步深入讨论，式(6)中稳定信道和随机信道分别可以表示为：
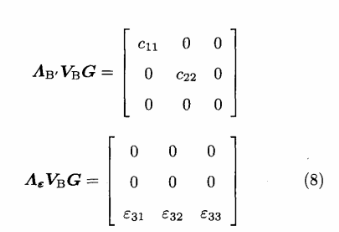
令Vbi为矩阵VB的第i个行向量，9i为加密矩阵Gr的第E个行向量，其中i-l，2，3．则由式(8)可以得到方程组：
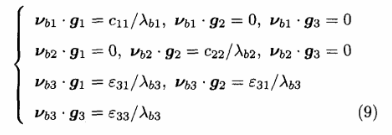
由式(9)可以看出，向量91在向量坳l方向上的投影为IIC11/\blll’在向量l)b2方向上的投影为O，在向量r)b3方向上的投影则为一随机数ltc3l/Ab311，其大小由91的方向和大小决定．可见91在由l/bl和Ub3张成的平面内，并且与Vb2垂直．91的起点位于原点而终点位于与Vb3平行且距离为llcll/At,ill的直线上，令Q= <gl，Vb3>，则有Q∈(0，7r)．类似可以得出92在由l/b2和I/b3张成的平面内，并且与l,bl垂直。92的起点位于原点而终点位于与Ub3平行且．距离为IIC22／入6211的直线上，令p- <g2，rib3），则有p∈(0，7r)．而g3则是与%3平行的一个向量，大小可随机设置.91、g2、93在l,bl、'Iib2 - Ub3构成空间的解集空间如图2所示。
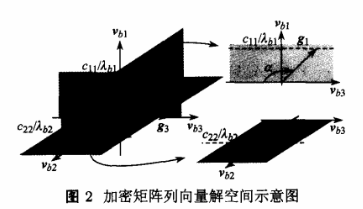
可见，在得到相同的常数矩阵C时，g1、g2. g3可以有无数种选取方式，加密矩阵G有足够的冗余空间。
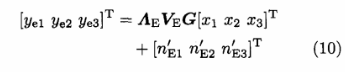
式(7)中，Eve的接收信号为YE=AEVEGX。在M=3时，经过加密矩阵G后，Eve的接收信号可以表示为： 令'Vel为矩阵VE的第茁个行向量，其中t=1，2，3，由式(10)整理可以得到:
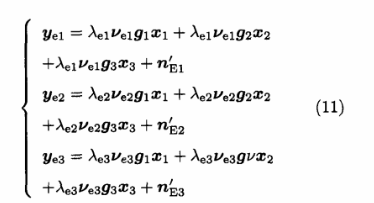
以上讨论了M=3时加密模块G的构造方法和经过加密模块后Eve接收信号的表达式，当M>3时，加密矩阵G有着相似的构造方法，不过由于维数的增加，矩阵G的列向量9i已经不能使用图2所示方法进行空间表示。但是，经过上述类似的推导，加密矩阵G依然需要满足与式(8)类似条件，有着近似的构造方法．同时，Eve的接收信号也可以得到与式(9)、(10)相似的结果。
三、系统保密容量
由信息论可以得到Bob的信息传输速率为：
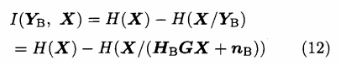
假设Bob的信道矩阵是M维的，则Bob共有M个子信道．本文中发送等概率二进制符号z∈t-1，1)且p(x -1)=p(x.= -1)=1/2，根据设计的算法可以得到：
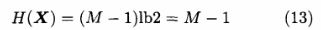
这样Alice-Bob信道的信息传输速率可以表示为：
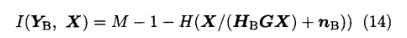
同样，可以得到Alice-Eve信道的信息传输速率为：
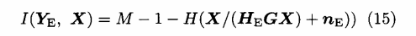
则系统信息安全传输速率为：
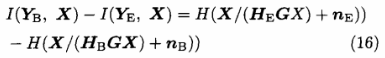
在本文的加密系统中，Bob端的信道转移矩阵是一个接近常数的矩阵，虽然存在信道噪声，但通信系统的误码率一般很低，并能通过请求重传等机制保证可靠接收。因此，可以认为Bob端在接收到信号YB之后就可以完全确定发送的信息X，对信源发送的信息已经没有任何疑义，于是可以得到：
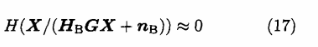
对于Eve来说，接收信号是随机变化的，这M-1个子信道每一个都是一个二进制信道，则有:
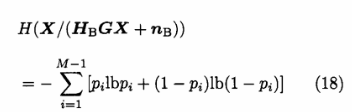
式中，pi为第茁个子信道翻转概率，所谓翻转概率是指信源发送1(或者-1)时，接收用户判为-1(或者1)的概率，可以看出Pi∈[0，1]，i∈[1，M-1]。特别的，当z=0时，取lbz=0。
综合等式(12)、(17)、(18)，可以得到系统的保密容量为：
式中，当所有Pi=1/2(i∈[1，M-1])时，等号成立。
对于信道矩阵为M维的二进制系统，理论上的最大传输速率是M bit/(s．Hz-1)。本文通过信道特征值分解提取弱特征进行随机加扰算法所得到的保密容量为(M -1)bit/(8．Hz-1)，系统的保密性能有所提升，但是系统的传输速率却有所降低，可见得到保密性能的提升是以牺牲一定的传输速率为代价的。
小知识之物理层
物理层（或称物理层，Physical Layer）是计算机网络OSI模型中最低的一层。物理层规定:为传输数据所需要的物理链路创建、维持、拆除，而提供具有机械的，电子的，功能的和规范的特性。简单的说，物理层确保原始的数据可在各种物理媒体上传输。局域网与广域网皆属第1、2层。
企业打印安全如何进行管理与防护
在信息技术迅猛发展的大背景下，打印设备作为数据信息最后输出的重要终端之一，其安全性、保密性日益受到企事业单位、政府机关的高度重视。
同时，从桌面打印机到复合一体机，从普通纸张打印到彩色纸张打印直至特种排版打印，企业在管理过程中所面对的管理对象变得日趋复杂。尤其是对于打印耗材的成本管控，更是一些中小型企业日常面临的难题。
更值得关注的是，在实际工作中大量打印作业涉及敏感信息，如产品报价、财务报表、员工工资单、方案标书等等，一旦未能妥善管理，就会造成企业机密泄露。
面对这些企业在日常办公中遇到的打印安全与管理难题，安企神软件可以对企业所有打印文件实现安全管控，在不改变原有打印习惯、不影响内部办公效率的前提下，添加水印信息溯源追踪；同时后台生成审计日志，对所有打印行为做到实施管控，严防核心数据文件在不知情的情况下被打印泄密，而且内部保留的审计日志，能在发生泄密事件后进行针对性追责、有效降低企业损失。
1、数据加密管理
对数据进行加密处理，从源头来保护核心数据，是解决泄密的最好方法，对于企业来说成本也较低。从数据的创建、存储、传输和处理等全生命周期进行加密保护，保证在打印之前数据都是加密状态下得到防护和管理。
2、严格权限控制
在安全打印管理策略的制定和实施中，遵循最小特权原则和最小泄露原则。同时可以设置多级安全策略，具有安全级别的信息资源，只有安全级别比他高的主体才能够访问然后进行打印，避免机密程度高的数据被多人访问、传输、和打印，造成泄露。
3、运用打印水印
可以在打印时自动添加水印，打印水印有效保证打印记录可追溯。后台采集打印信息，包括每次打印的打印机、用户名、计算机名、打印页数、打印份数、打印时间、文档名称、文档内容等汇总审计，帮助企业减少打印纸张铺张浪费的现象，降低企业打印成本。
4、强化日志审计
审计是对访问控制的必要补充，是访问控制的一个重要内容。可以通过审计日志了解到所有内部打印动作、操作终端、打印内容等，知道打印文件的来源途径，为后续可能发生的数据安全事件进行追责定位，减少损失。
安企神软件可以有效地保证企业安全打印管理，封堵打印输出泄露、遗失的途径，并通过审计证据迅速定位事故源头，从事前、事中、事后三个层面保障打印安全，补足数据安全体系漏洞，夯实企业整体数据安全防护能力。
本文为收集整理，文章部分观点不代表本站观点，如有侵权或其它问题请反馈客服。https://www.wgj7.com/cjwt/16468.html